ActivityPub is a technical specification towards decentralized (more precisely, federated) social networking (termed the Fediverse) based upon the exchange of ActivityStreams messages that follow the Activity Vocabulary. The ActivityPub proposal has been standardized and published by the W3C and has motivated the design of several federated social networking systems. NB: As Open Risk we are already present on the Fediverse via a Mastodon account.
Analysing and understanding the dynamics of economic networks is of vital importance for informed decision-making. In a number of previous White Papers we reviewed and illustrated how mathematical concepts from Network and Graph theory (OpenRiskWP08,OpenRiskWP10) can be used to that effect.
Our focus in the latest White Paper (OpenRiskWP15) in the Connect the Dots series is on mathematical (in particular Tensor) representations of federated online networks that help encode succinctly certain important elements of their structure. We focus on federated networks adhering to the ActivityPub protocol, which we discuss in the relevant detail.
The classic, simple (with no self-loops), directed graph is sufficient to describe the Following/Followed connectivity of Actors within a single Server. The core idea is to map Actors to graph nodes, and express relations using graph edges.
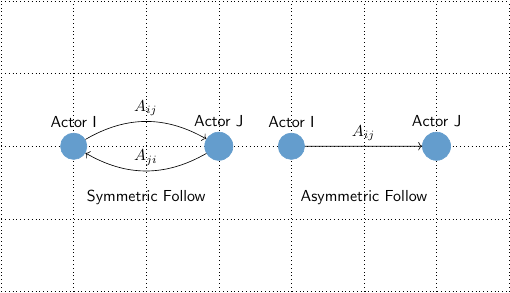
The challenge is that actual ActivityPub networks will be quite a bit more demanding in the variety of Actor and Activities that they engage in, which limits the utility of simple graphs.
Loosely speaking, Tensors can be seen as generalizations of vectors and matrices. Vectors could be called rank-1 tensors, they have one index. Matrices are rank-2 tensors, they have two indexes or dimensions. The more indices, the higher the rank of a tensor. Adjacency Matrices are rank-2 tensors, so they are inherently limited in the complexity of the relationships they can capture. Adjacency Tensors are higher-order objects that can potentially capture more complex network relations. The multilayer adjacency tensor is a very general object that can be used to represent a wealth of complicated relationships among nodes.
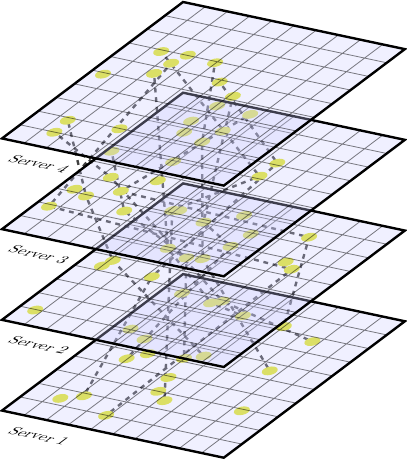
The mapping of networks to tensor algebra is typically the first step in the process towards concrete applications. Depending on the task one might need to flatten the relevant tensors into the so-called supra-adjacency matrix which can then be analysed with more conventional matrix algebra.